26) Bonds
Bonds of 10: Bonds Building a Wall
Mathematics
Develop the concept of:
- The whole of 10 being equal to two parts joined together.
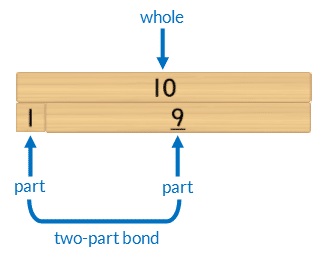
The two parts bond (join) together to become equal to the length of the whole.
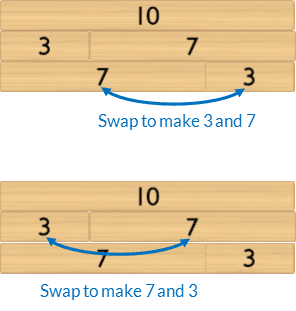
- The Commutative Property of Addition: swapping the order of the parts does not alter the size of the whole. For example, changing the order of the parts of 3 and 2 to 2 and 3 does not alter the size of the whole.
- Mathematics as the science of pattern.
Language
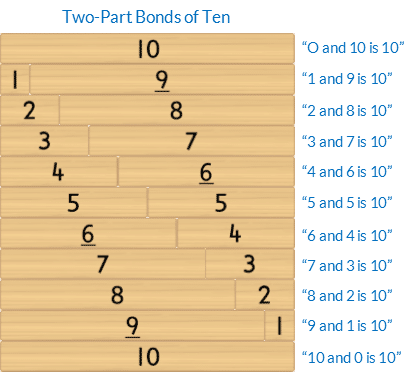
- “(Part) and (part) is (whole)”. eg “4 and 6 is 10”
- addition as “and” when joining parts
- equals as “is”, “is equal to”
- bond
- too long, too big, too short, too small
- commutative property
- row (horizontal)

Differentiation
A little easier
Scaffold: counting order
Scaffold finding the Bonds of 10 in counting order.
- Place the 10 block horizontally in front of the student.
- Then place the 1 block underneath the 10. Ask the student, “Which number joins with 1 to make it the same as 10?” Model saying the bond, whilst touching the related blocks, “Yes, 1 and 9 is 10”
- Repeat this process with each block in counting order.
Skill Focus: commutative property of addition
Represent the commutative propert of addition by focusing on one two-part bond at a time. Use the 10 block as the whole.
- Begin with the bond of 1 and 9. Place both rows of related two-part bonds beneath the whole. Then rearrange the parts within each row to make their order the same.
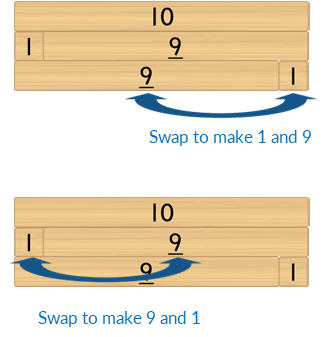
- Repeat for the bond of 2 and 8.
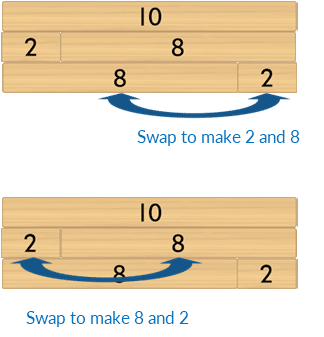
- Repeat for the bond of 3 and 7, and finally 4 and 6.
A little harder
Recall Practice: fluency packing away
Develop fluency with bonds of 10 when packing away. Cover the template with a piece of white paper. Students pick up one block randomly then find its bond of ten.
Recall Practice: missing Bond Block
Develop fluency recalling two-part bonds of 10.
An activity for pairs. Instruct students to:
- Build a wall of 10 with rows in random order.
- When the wall is complete one student closes their eyes whilst the other removes, and hides, one block from each row.
- The student opens their eyes and identifies the missing block from each row, verbalising the bond. For example, “2 and 8 is 10.”
- The student who removed the blocks returns the missing block saying, “Yes, 2 and 8 is 10”.
- Swap roles.

Three-Part Bond
Instruct students to build one row of ten with three blocks (parts).
- Select one row.
- Work mathematically by moving the blocks in a systematic order to list all the addition combinations for that bond.
For example, 1+2+7 is equal to 1+7+2 and 2+1+7 and 2+7+1 and 7+1+2 and 7+2+1
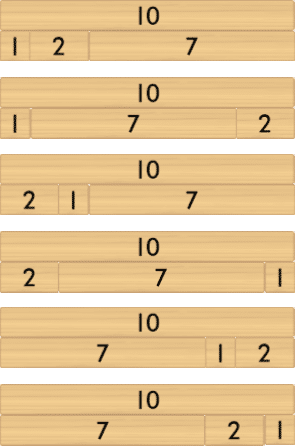

The associative property of addition: three or more parts can be added in any order without changing the size of the whole.
Progression
In the next activity students develop fluency with bonds of 10. Go to
Activity 27
Bonds of 10: Fluency, Filling a Wall

