53) Bridging Ten Subtraction
Ten Plus Bonds: Strategy Taking Away
Mathematics
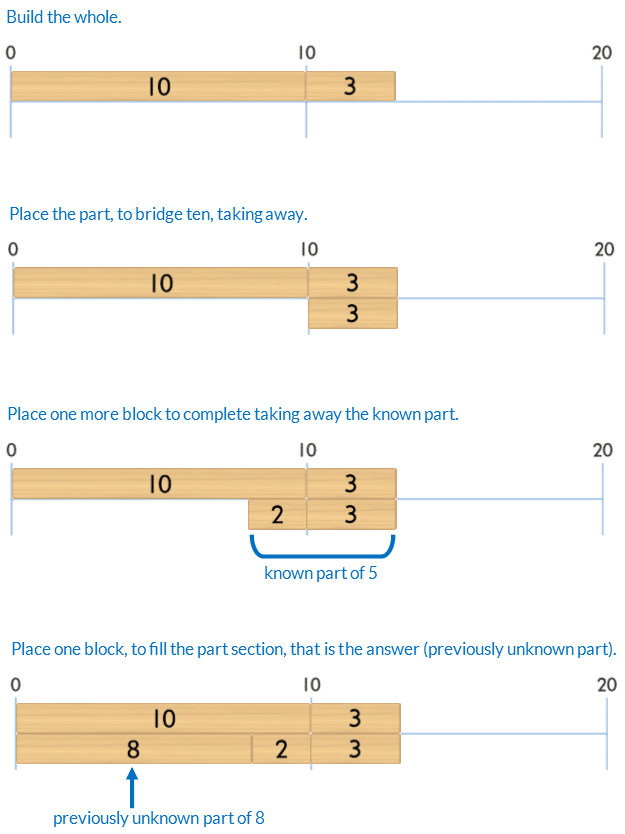
Develop the strategy of bridging ten to subtract, using taking away, for wholes up to 20.
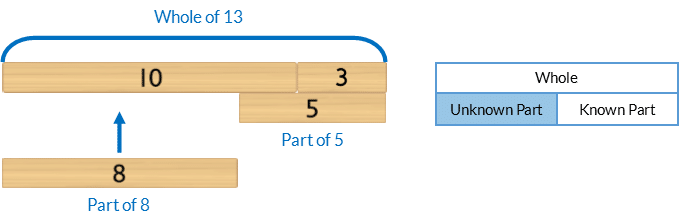
For example, to solve 13 – 5
Prior knowledge of part-part-whole, bonds of 10 and place value partitioning using ten plus bonds is needed.
Language
- bridge ten
- subtract
- taking away
- equals
- left
Note, in this activity students are finding a missing part in a subtraction equation.
They are NOT completing “sums”. The “sum” is the whole, found by adding the parts.
The word ‘sum’ is often incorrectly used when the word ‘equation’ is meant. It is impossible to “complete a subtraction sum”.


Differentiation
A little easier
Scaffold: counting order
Calculate each question in counting order, working clockwise around the spinner, from the 12 o’clock position. Do not flick the spinner. Assist students to identify patterns.
Sequence: step by step
If students have difficulty partitioning the part being taken away to bridge ten, use an additional block.
For example, to model 13 – 5
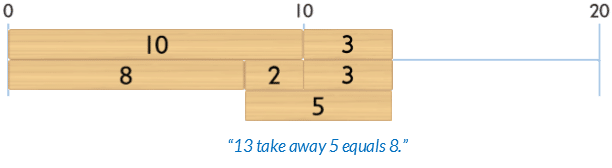
Some students find it conceptually easier to first place the block representing the part being taken away. Then place the blocks this is partitioned into to bridge ten on top of this block.
- From a top view they can see the bridging ten partition, of 3 and 2.
- From a front view they can see the part 5.

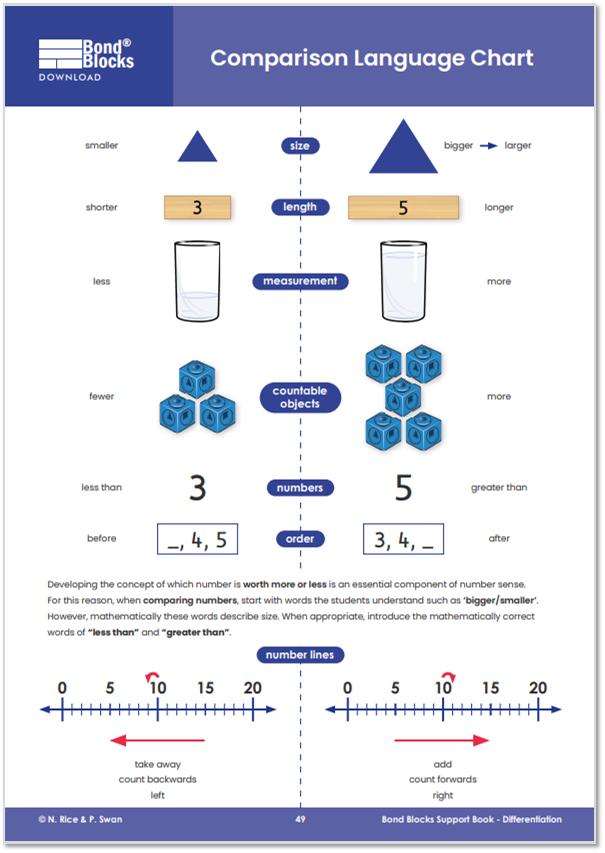
Directional Support: desk visual
Click to download a Comparison and Number line Language: Desk Visual to support students who have directional and sequencing difficulties.
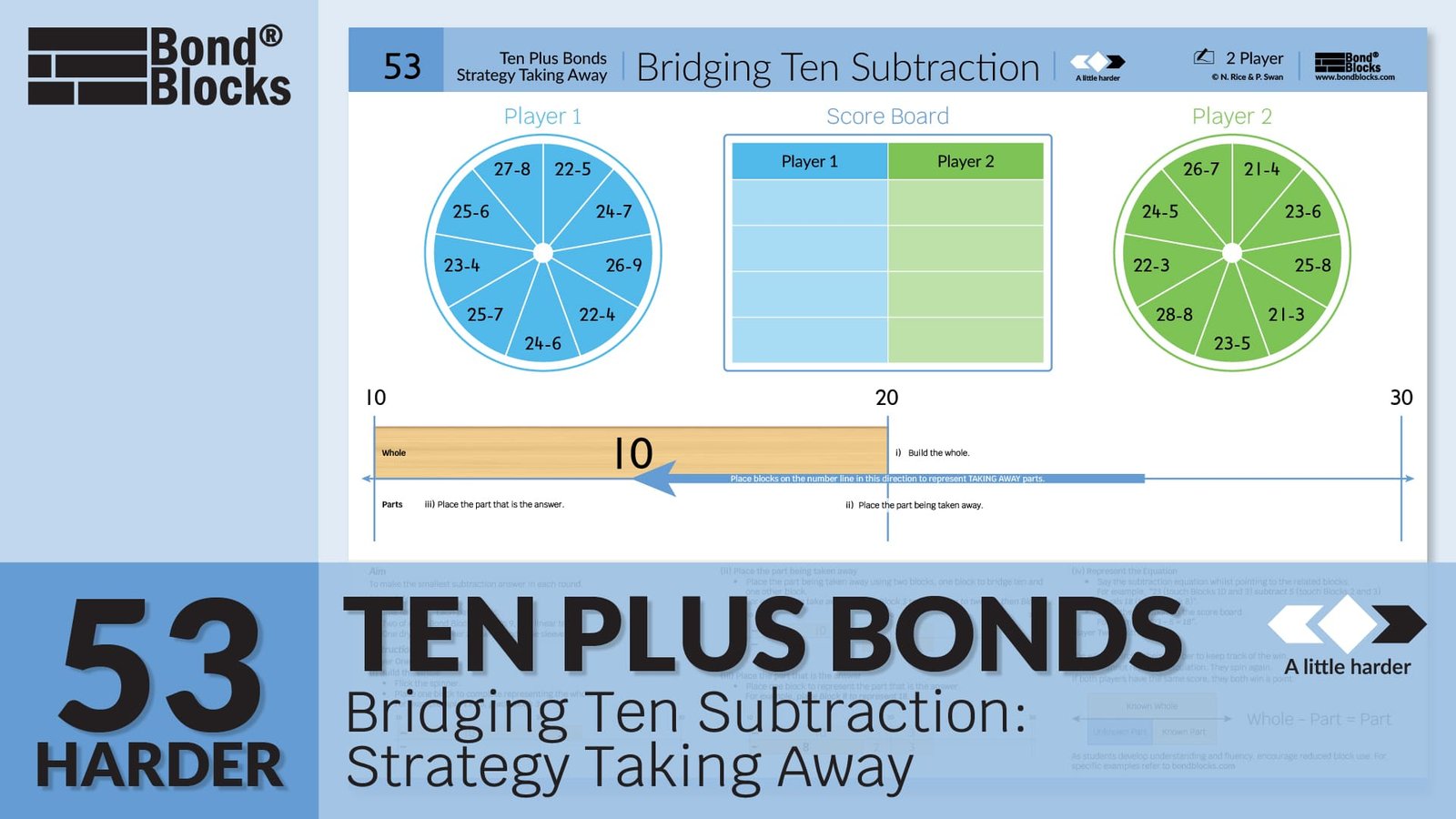
A little harder
Bridging ten subtraction strategy taking away
Play “Ten Plus Bonds: Bridging Ten Subtraction Strategy Taking Away a little harder”. In this game students have to solve subtraction by bridging ten, to twenty, for wholes up to 30.
Reduce Scaffolds
The blocks are a scaffold to support calculation. If students can calculate without some or all of the blocks encourage this. Below is a progression of reducing scaffolding, from most to least support, using bridging ten for 23-5.
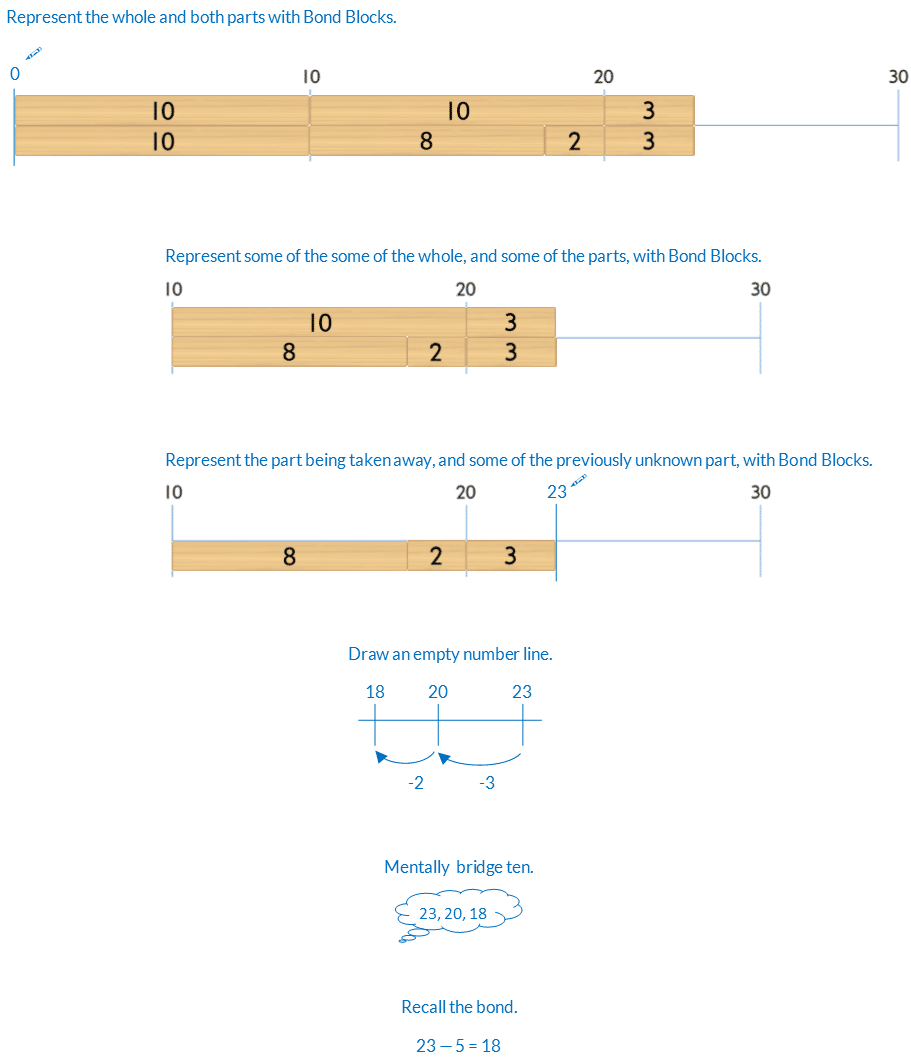
Progression
In the next activity students solve subtraction bridging ten, but instead of taking away they add on. Go to
Activity 54
Ten Plus Bonds: Bridging Ten Subtraction, Strategy Adding On
