Shop

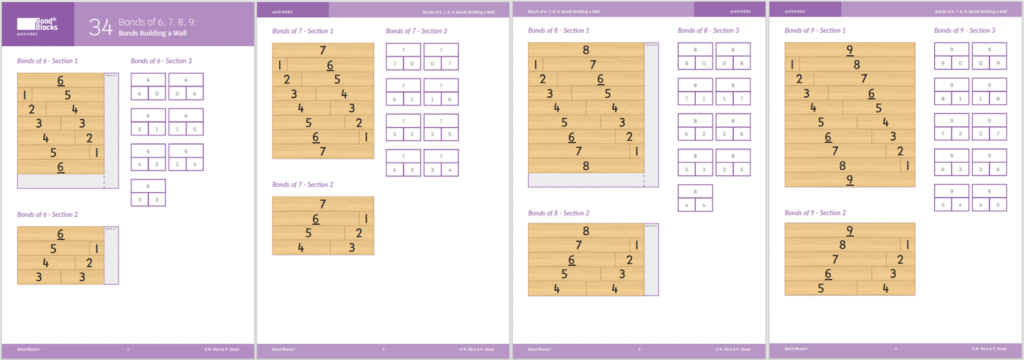
34 Bonds

Bonds of 6, 7, 8, 9: Building a Wall

Section 1a: Build A Wall

Section 1b: Order The Wall

Section 1c: Verbalise Two-Part Bonds

Section 2: Commutative Property of Addition

Section 3: Part-Part-Whole

Mathematics

Develop the concept of:

  • The whole of 6, 7, 8 or 9 being equal to two parts joined together.

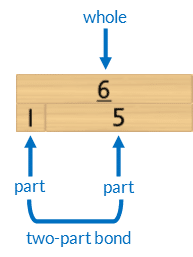
The two parts bond (join) together to become equal to the length of the whole.

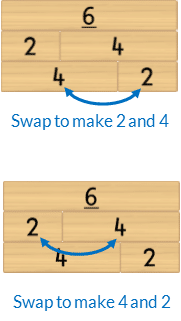
  • The Commutative Property of Addition: swapping the order of the parts does not alter the size of the whole. For example, changing the order of the parts of 3 and 2  to 2 and 3 does not alter the size of the whole.
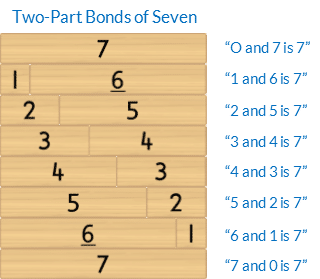
  • Mathematics as the science of pattern. In Activity 34 students identify all two-part bonds for the wholes of 6,7,8 and 9 because they use patterns to develop mathematical understandings. Please be aware that students will already be fluent with double bonds and five plus bonds from previous chapters as well as bonds that use zero and one as a part. This leaves the remaining two-part bonds, highlighted in purple shading, to focus on developing fluency with in the remaining activities in this chapter. 

Language

  • “(Part) and (part) is (whole)”. eg “4 and 6 is 10”
  • addition as “and” when joining parts
  • equals as “is”, “is equal to” 
  • bond
  • too long, too big, too short, too small
  • commutative property
  • row (horizontal)

Core Activity Support Materials

Click to open answers in a new tab.

Differentiation

A little easier

Counting order

Choose the whole of 6, 7, 8 or 9. Scaffold finding the Bonds of this whole in counting order.

  • Place the block representing the whole horizontally in front of the student.
  • Then place the 1 block underneath the whole. Ask the student, “Which number joins with 1 to make it the same as [6/7/8/9]?” Model saying the bond, whilst touching the related blocks,. For example, “Yes, 1 and 5 is 6”.
  • Repeat this process with each block in counting order.
Represent two-part bonds with two hands

Students can represent many two-part bonds of the wholes 6, 7,8  and 9 with their hands. Students use their fingers in a subitised way, not counting by ones. The fingers held up on each hand represent each part of the two-part bond. 

Note, not all two-part bonds can be represented this way. For example, eight as six and two.

 

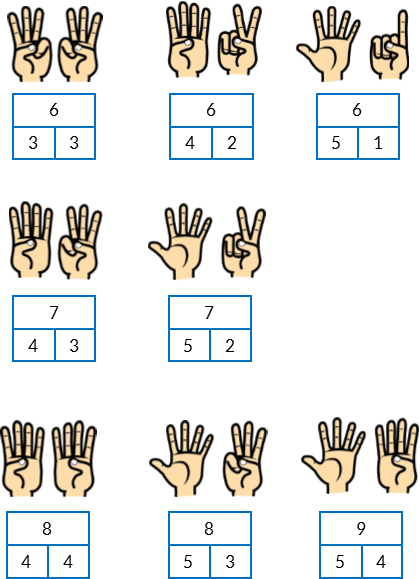
Start with 6. Write this on a piece of paper or the board. Define this as the whole amount.

  • Ask students to make this using their fingers. Record this partition in a Part-Part-Whole diagram.
  • Encourage students to make it another way and another until they have identified each bond.

Repeat for the whole of 7.

Develop fluency by calling out a number from 6 to 9 at random and instructing students to represent this number with their fingers. Their representation must be different from the person sitting next to them. Each student verbalises the bond they have made. For example, “8 is 5 and 3.” If both students make the same representation they each need to have another go using a different representation. 

Click this link to read Teacher Notes for more information about using fingers to “Develop Calcuation, Not Counting”. 

A little harder

Missing part

Develop fluency recalling two-part bonds of the whole 6, 7, 8 or 9.

An activity for pairs. Instruct students to:

  • Build a wall for the chosen whole, in random order. Place this on the frame of Activity One. When building the wall first place the block representing the whole in the top row. Then take turns to build each row after that, in random order, by picking up a block and then finding the other block that joins with it to build the whole. 
  • When the wall is complete one student closes their eyes whilst the other removes, and hides, one block from each row.
  • The student opens their eyes and identifies the missing block from each row, verbalising the bond. For example, “2 and 4 is 6.”
  • The student who removed the blocks returns the missing block saying, “Yes, 2 and 4 is 6”. 
  • Swap roles.
Three-part bonds

Instruct students to build one row of either 6, 7, 8 or 9 with three blocks (parts).

  • Select one row.
  • Work mathematically by moving the blocks in a systematic order to list all the addition combinations for that bond.

For example, 1+2+3 is equal to 1+3+2 and 2+1+3 and 2+3+1 and 3+1+2 and 3+2+1

The associative property of addition: three or more parts can be added in any order without changing the size of the whole.

Progression

In the next activity students apply bonds of 6, 7, 8 and 9 to subtraction. Go to

Activity 35i

Bonds of 6, 7, 8, 9: Subtraction Building a Wall